Treap

Harry Huang (aka Wenyuan Haung, 黄问远) Lv1
  2024-11-07 01:35:27 2024-11-07 01:35:27 Created   2024-11-15 20:16:23 2024-11-15 20:16:23 Updated  

##前置芝士
熟练掌握二叉查找（排序）树的插入、删除、求排名、求某一排名的数、求前驱、求后继等操作。
#引言
二叉查找树看似可以在 $O(logn)$ 中完成任意上述操作。但若该二叉查找树退化为如下形态：

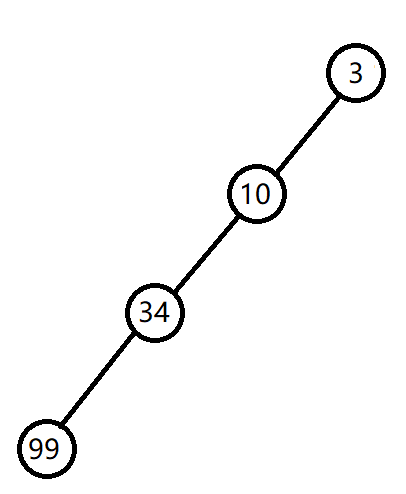
此时，在此图上操作的时间复杂度仍为 $O(n)$。
观察可知：二叉查找树的最优形态是平衡树，故需要一种能维持树的平衡形态的二叉查找树。

#正文
Treap又名树堆，是一种利用随机性来维持二叉查找树的平衡形态的树（相较于Splay，方便且暴力许多）。
学习Treap，首先需要了解Treap的特色旋转操作（与Splay的旋转有一定差别）。旋转操作在Treap中主要用于在不破坏二叉查找树的性质（左子树比根小，右子树比根大）的情况下，对元素的位置进行挪动。根据所需旋转的节点属于其父亲节点的左子树和右子树，可分为左旋和右旋。

###旋转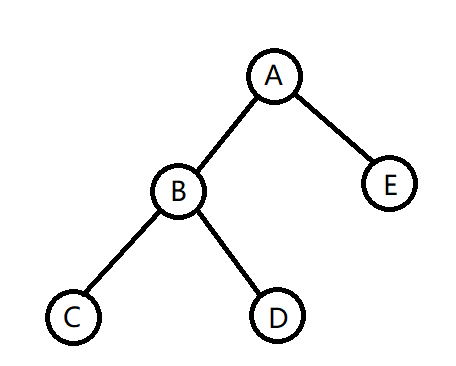

如图，假设我们要将B点挪到现A点的位置，一种很自然的思路是将图整体像右移动：C点移至原B点位置、B点移至原A点位置、A点移至原E点位置、E点移至原E点右儿子位置。
但此时会出现一个问题，如图：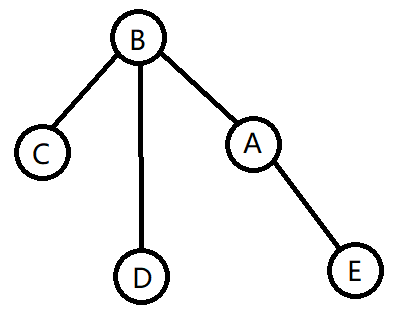

B点有两个右儿子：A、D，故需要将一个右儿子移至他处。发现A点没有左儿子，所以可将D点改为A点的左儿子。
操作完成后可发现，子树的二叉查找性并没有受到破坏，所以旋转可以随意在二叉查找树中使用。
因为该操作的过程类似旋转，并且方向为顺时针，故称其为右旋。
左旋与右旋类似，故在此不赘述。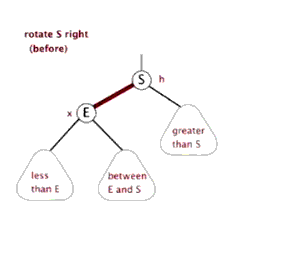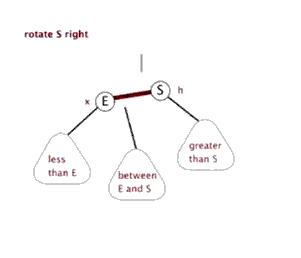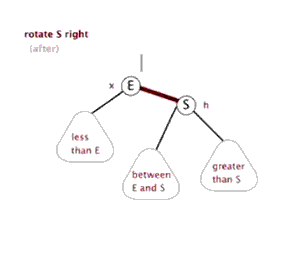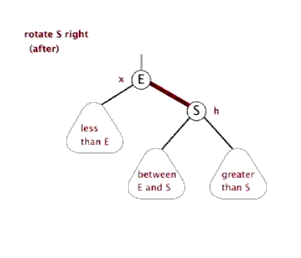

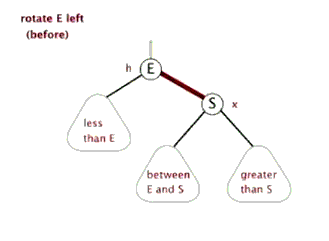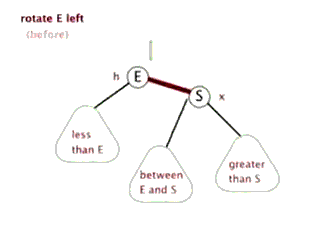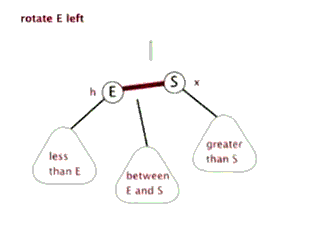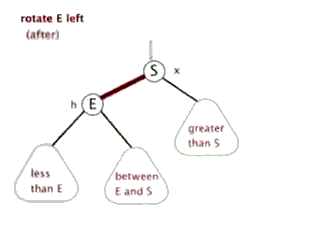
GIF来自https://www.cnblogs.com/lazy-people/p/9326556.html

这两张动图可以更方便读者理解“旋转”操作的过程。
####代码
1
2
3
4
5
6
7
8
9
void rotate (int &x, int d) {
    int t = sons[x][d ^ 1];
    sons[x][d ^ 1] = sons[t][d];
    sons[t][d] = x;
    pushup (x);
    pushup (t);
    x = t;
    return ;
}

###插入节点
Treap的插入操作与普通的二叉查找树如出一辙，但是为了保持平衡，每个节点会有一个随机值来保证图的形态的随机性。
###操作步骤
#####1、从根节点开始递归；
#####2、如果当前节点的值等于需插入的值，则将该节点的数值数量和该节点的子树的节点数+1；
#####3、如果当前节点的值大于需插入的值，则在当前节点的左儿子中继续2、3两步；如果当前节点的值小于需插入的值，则在当前节点的右儿子中继续2、3两步。操作完成后，若子节点的随机值大于当前节点的随机值，则将当前节点向下旋转；
#####4、如果当前节点为空节点，则在当前节点中建立新的节点，并赋予新节点一个随机值；
####代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void ins (int &p, int x) {
    if (!p) {
        p = ++ cnt;
        siz[p] = num[p] = 1;
        val[p] = x;
        rd[p] = rand ();
        return ;
    }
    if (val[p] == x) {
        num[p] ++;
        siz[p] ++;
        return ;
    }
    int d = (x > val[p]);
    ins (sons[p][d], x);
    if (rd[p] < rd[sons[p][d]])
        rotate (p, d ^ 1);
    pushup (p);
    return ;
}

###删除节点
删除操作和插入节点的区别在于，需要分类讨论需删除的节点的状态（左儿子存在与否、右儿子存在与否）。

#####情况一：左儿子右儿子都不存在
因为叶子节点的存在不会影响整树的平衡，所以此时可以直接删除该节点；
#####情况二：左儿子存在、右儿子不存在
若直接删除节点，有可能影响树的平衡性，所以将当前节点向左儿子旋转；
#####情况三：左儿子不存在，右儿子存在
与情况二大同小异，差别是要将当前节点向右儿子旋转；
#####情况四：左儿子存在，右儿子存在
此时需要选择旋转左旋还是右旋。显然，若进行左/右旋，则左/右儿子会更替当前节点的位置。故为了维持树的随机性，需要将左儿子和右儿子中随机值大的点向上旋转；

点的遍历操作与插入节点的遍历如出一辙，此处不再赘述。
####代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void del (int &p, int x) {
    if (!p)
        return ;
    if (x < val[p])
        del (sons[p][0], x);
    else if (x > val[p])
        del (sons[p][1], x);
    else {
        if (!sons[p][0] && !sons[p][1]) {
            num[p] --;
            siz[p] --;
            if (num[p] == 0)
                p = 0;
        }
        else if (sons[p][0] && !sons[p][1]) {
            rotate (p, 1);
            del (sons[p][1], x);
        }
        else if (!sons[p][0] && sons[p][1]) {
            rotate (p, 0);
            del (sons[p][0], x);
        }
        else if (sons[p][0] && sons[p][1]) {
            int d = (rd[sons[p][0]] > rd[sons[p][1]]);
            rotate (p, d);
            del (sons[p][d], x);
        }
    }
    pushup (p);
    return ;
}

###查找某个数的排名
仍然可以使用正常的二叉排序树的一般遍历方式。

###遍历操作
###情况一：若当前节点的值等于查找的树，则返回当前节点的左子树的数量+1；
###情况二：若当前节点的值小于需查找的值，则返回 需查找的值在右子树的排名+当前节点的左子树的节点数+当前节点的数量；
###情况三：若当前节点的值大于需查找的值，则返回 需查找的值在左子树的排名；

####代码
1
2
3
4
5
6
7
8
9
10
int ranks (int p, int x) {
    if (!p)
        return 0;
    if (x == val[p])
        return siz[sons[p][0]] + 1;
    if (val[p] < x)
        return siz[sons[p][0]] + num[p] + ranks (sons[p][1], x);
    if (val[p] > x)
        return ranks (sons[p][0], x);
}

###查找某排名的数
本质就是逆向操作“查找某个数的排名”。

####代码
1
2
3
4
5
6
7
8
9
10
int find (int p, int x) {
    if (!p)
        return 0;
    if (x <= siz[sons[p][0]])
        return find (sons[p][0], x);
    else if (x > siz[sons[p][0]] + num[p])
        return find (sons[p][1], x - siz[sons[p][0]] - num[p]);
    else
        return val[p];
}

###求先驱、后继
过程并不复杂：在遍历过程中不断向需求先驱的数靠近，同时用当前节点的值更新答案。

####代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int pre (int p, int x) {
    if (!p)
        return -inf;
    if (val[p] >= x)
        return pre (sons[p][0], x);
    else
        return max (val[p], pre (sons[p][1], x));
}
int suc (int p, int x) {
    if (!p)
        return inf;
    if (val[p] <= x)
        return suc (sons[p][1], x);
    else
        return min (val[p], suc (sons[p][0], x));
}

完整版代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 500, inf = 2000000005;
int n, rt, val[N], siz[N], rd[N], cnt, sons[N][2], num[N];
void pushup (int x) {
    siz[x] = siz[sons[x][0]] + siz[sons[x][1]] + num[x];
    return ;
}
void rotate (int &x, int d) {
    int t = sons[x][d ^ 1];
    sons[x][d ^ 1] = sons[t][d];
    sons[t][d] = x;
    pushup (x);
    pushup (t);
    x = t;
    return ;
}
void del (int &p, int x) {
    if (!p)
        return ;
    if (x < val[p])
        del (sons[p][0], x);
    else if (x > val[p])
        del (sons[p][1], x);
    else {
        if (!sons[p][0] && !sons[p][1]) {
            num[p] --;
            siz[p] --;
            if (num[p] == 0)
                p = 0;
        }
        else if (sons[p][0] && !sons[p][1]) {
            rotate (p, 1);
            del (sons[p][1], x);
        }
        else if (!sons[p][0] && sons[p][1]) {
            rotate (p, 0);
            del (sons[p][0], x);
        }
        else if (sons[p][0] && sons[p][1]) {
            int d = (rd[sons[p][0]] > rd[sons[p][1]]);
            rotate (p, d);
            del (sons[p][d], x);
        }
    }
    pushup (p);
    return ;
}
void ins (int &p, int x) {
    if (!p) {
        p = ++ cnt;
        siz[p] = num[p] = 1;
        val[p] = x;
        rd[p] = rand ();
        return ;
    }
    if (val[p] == x) {
        num[p] ++;
        siz[p] ++;
        return ;
    }
    int d = (x > val[p]);
    ins (sons[p][d], x);
    if (rd[p] < rd[sons[p][d]])
        rotate (p, d ^ 1);
    pushup (p);
    return ;
}
int ranks (int p, int x) {
    if (!p)
        return 0;
    if (x == val[p])
        return siz[sons[p][0]] + 1;
    if (val[p] < x)
        return siz[sons[p][0]] + num[p] + ranks (sons[p][1], x);
    if (val[p] > x)
        return ranks (sons[p][0], x);
}
int find (int p, int x) {
    if (!p)
        return 0;
    if (x <= siz[sons[p][0]])
        return find (sons[p][0], x);
    else if (x > siz[sons[p][0]] + num[p])
        return find (sons[p][1], x - siz[sons[p][0]] - num[p]);
    else
        return val[p];
}
int pre (int p, int x) {
    if (!p)
        return -inf;
    if (val[p] >= x)
        return pre (sons[p][0], x);
    else
        return max (val[p], pre (sons[p][1], x));
}
int suc (int p, int x) {
    if (!p)
        return inf;
    if (val[p] <= x)
        return suc (sons[p][1], x);
    else
        return min (val[p], suc (sons[p][0], x));
}
int main () {
    scanf ("%d", &n);
    for (int i = 1; i <= n; i ++) {
        int op, x;
        scanf ("%d%d", &op, &x);
        if (op == 1)
             ins (rt, x);
        else if (op == 2)
             del (rt, x);
        else if (op == 3)
             printf ("%d\n", ranks (rt, x));
                else if (op == 4)
             printf ("%d\n", find (rt, x));
                else if (op == 5)
             printf ("%d\n", pre (rt, x));
                else if (op == 6)
             printf ("%d\n", suc (rt, x));
    }
    return 0;
}

例题推荐：LOJ #104 普通平衡树

  • Title: Treap
  • Author: Harry Huang (aka Wenyuan Haung, 黄问远)
  • Created at : 2024-11-07 01:35:27
  • Updated at : 2024-11-15 20:16:23
  • Link: https://whuang369.com/2024/11/07/Treap/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
Treap
  1. 这两张动图可以更方便读者理解“旋转”操作的过程。####代码123456789void rotate (int &x, int d) { int t = sons[x][d ^ 1]; sons[x][d ^ 1] = sons[t][d]; sons[t][d] = x; pushup (x); pushup (t); x = t; return ;}
  2. ###插入节点Treap的插入操作与普通的二叉查找树如出一辙，但是为了保持平衡，每个节点会有一个随机值来保证图的形态的随机性。###操作步骤#####1、从根节点开始递归；#####2、如果当前节点的值等于需插入的值，则将该节点的数值数量和该节点的子树的节点数+1；#####3、如果当前节点的值大于需插入的值，则在当前节点的左儿子中继续2、3两步；如果当前节点的值小于需插入的值，则在当前节点的右儿子中继续2、3两步。操作完成后，若子节点的随机值大于当前节点的随机值，则将当前节点向下旋转；#####4、如果当前节点为空节点，则在当前节点中建立新的节点，并赋予新节点一个随机值；####代码1234567891011121314151617181920void ins (int &p, int x) { if (!p) { p = ++ cnt; siz[p] = num[p] = 1; val[p] = x; rd[p] = rand (); return ; } if (val[p] == x) { num[p] ++; siz[p] ++; return ; } int d = (x > val[p]); ins (sons[p][d], x); if (rd[p] < rd[sons[p][d]]) rotate (p, d ^ 1); pushup (p); return ;}
  3. 点的遍历操作与插入节点的遍历如出一辙，此处不再赘述。####代码12345678910111213141516171819202122232425262728293031void del (int &p, int x) { if (!p) return ; if (x < val[p]) del (sons[p][0], x); else if (x > val[p]) del (sons[p][1], x); else { if (!sons[p][0] && !sons[p][1]) { num[p] --; siz[p] --; if (num[p] == 0) p = 0; } else if (sons[p][0] && !sons[p][1]) { rotate (p, 1); del (sons[p][1], x); } else if (!sons[p][0] && sons[p][1]) { rotate (p, 0); del (sons[p][0], x); } else if (sons[p][0] && sons[p][1]) { int d = (rd[sons[p][0]] > rd[sons[p][1]]); rotate (p, d); del (sons[p][d], x); } } pushup (p); return ;}
  4. ####代码12345678910int ranks (int p, int x) { if (!p) return 0; if (x == val[p]) return siz[sons[p][0]] + 1; if (val[p] < x) return siz[sons[p][0]] + num[p] + ranks (sons[p][1], x); if (val[p] > x) return ranks (sons[p][0], x);}
  5. ####代码12345678910int find (int p, int x) { if (!p) return 0; if (x <= siz[sons[p][0]]) return find (sons[p][0], x); else if (x > siz[sons[p][0]] + num[p]) return find (sons[p][1], x - siz[sons[p][0]] - num[p]); else return val[p];}
  6. ####代码12345678910111213141516int pre (int p, int x) { if (!p) return -inf; if (val[p] >= x) return pre (sons[p][0], x); else return max (val[p], pre (sons[p][1], x));}int suc (int p, int x) { if (!p) return inf; if (val[p] <= x) return suc (sons[p][1], x); else return min (val[p], suc (sons[p][0], x));}